

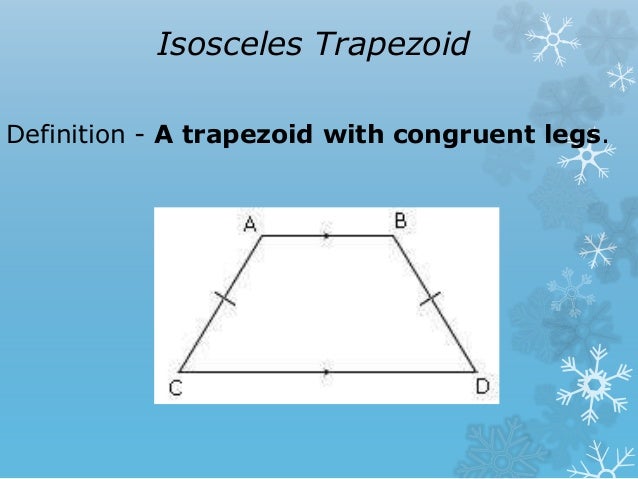
In fact, this value is crucial when we discuss how to calculate the area of a trapezoid and therefore gets its own dedicated section. The height of a trapezoid is the distance between the bases, i.e., the length of a line connecting the two, which is perpendicular to both. Quite a fancy definition compared to the usual one, but it sure makes us sound sophisticated, don't you think?īefore we move on to the next section, let us mention two more line segments that all trapezoids have. Indeed, if someone didn't know what a rectangle is, we could just say that it's an isosceles trapezoid which is also a right trapezoid. With these special cases in mind, a keen eye might observe that rectangles satisfy conditions 2 and 3. Secondly, observe that if a leg is perpendicular to one of the bases, then it is automatically perpendicular to the other as well since the two are parallel. Firstly, note how we require here only one of the legs to satisfy this condition – the other may or may not. We've already mentioned that one at the beginning of this section – it is a trapezoid that has two pairs of opposite sides parallel to one another.Ī trapezoid whose legs have the same length (similarly to how we define isosceles triangles).Ī trapezoid whose one leg is perpendicular to the bases. We'd like to mention a few special cases of trapezoids here.
The two other non-parallel sides are called legs (similarly to the two sides of a right triangle). Usually, we draw trapezoids the way we did above, which might suggest why we often differentiate between the two by saying bottom and top base. the angle at the extremities of one base are 65 degree and 45 degree respectively.The two sides, which are parallel, are usually called bases. The base of a trapezoid are 22 and 12 respectively. how fast is the water level rising when the water is running into the trough at a rate of 1 cubic foot per minute. The cross section of a 5-ft long trough is an isosceles trapezoid with a 2 foot lower base, a 3-foot upper base, and an altitude of 2 feet. Which description does NOT guarantee that a trapezoid is isosceles? A. If AB = 5x - 9, DC = x + 3, and EF = 2x + 2, what is the value of x? In the diagram, EF is the median of trapezoid ABCD. How many lines of symmetry could an isosceles trapezoid have? If the areas of triangles ABP and CDP are 8 and 18, respectively, then find the area of trapezoid ABCD.
Let P be the intersection of diagonals AC and BD. The bases of trapezoid ABCD are AB and CD. The smaaler trapezoid is 24m, and the larger trapezoid is 57m. Find the area of the larger trapezoid to the nearest whole number. The area of the smaller trapezoid is 564m^2. Given: ABCD is a trapezoid, AB = CD, BK ⊥ AD (they are perpendicular, AK = 10, KD = 20 Find: BC AD I got that BC is 15 and AD is 35 so I got BC/AD=15/35 is this answer right? and is so can you add the answer and an explanation The angles at the extremities of one base are 65 degree and 40 degree respectively find the two legs. The bases of a trapezoid are 22 and 12 respectively. We are given that $CD = 8$, $AD = BC = 7$, and $BD = 9$. The bases of trapezoid $ABCD$ are $\overline$.


 0 kommentar(er)
0 kommentar(er)
